By far the most important physical property of particulate samples is particle size. Measurement of particle size distributions is routinely carried out across a wide range of industries and is often a critical parameter in the manufacture of many products. Measuring particle size distributions and understanding how they affect your products and processes can be critical to the success of many manufacturing businesses.
Particle size influences many properties of particulate materials and is a valuable indicator of quality and performance. This is true for powders, suspensions, emulsions, and aerosols. The size and shape of powders influence the flow and compaction properties. Powder or droplets in the range of 2-5 μm aerosolize better and will penetrate into lungs deeper than larger sizes. For these and many other reasons, it is important to measure and control the particle size distribution of any products.
There are also industry/application-specific reasons why controlling and measuring particle size is important. In the paint and pigment industries particle size influences appearance properties including gloss and tinctorial strength. The particle size of the cocoa powder used in chocolate affects color and flavor. The size and shape of the glass beads used in highway paint impact reflectivity. Cement particle size influences hydration rate & strength. In the pharmaceutical industry, the size of active ingredients influences critical characteristics including content uniformity, dissolution, and absorption rates. Other industries where particle size plays a key role include nanotechnology, proteins, cosmetics, polymers, soils, abrasives, fertilizers, and many more.
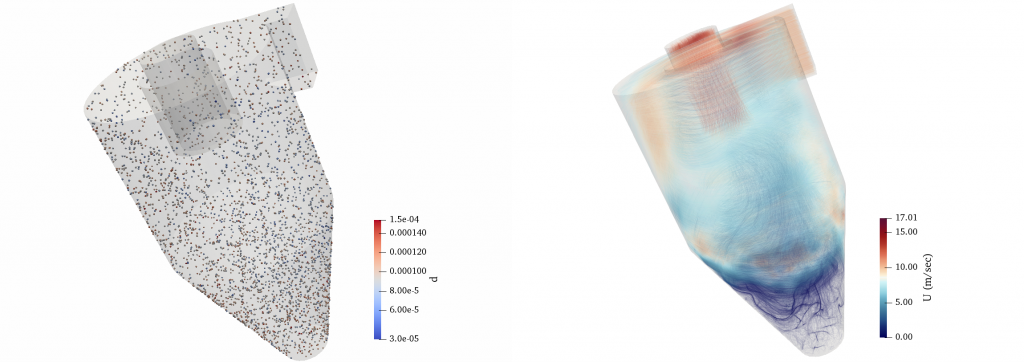
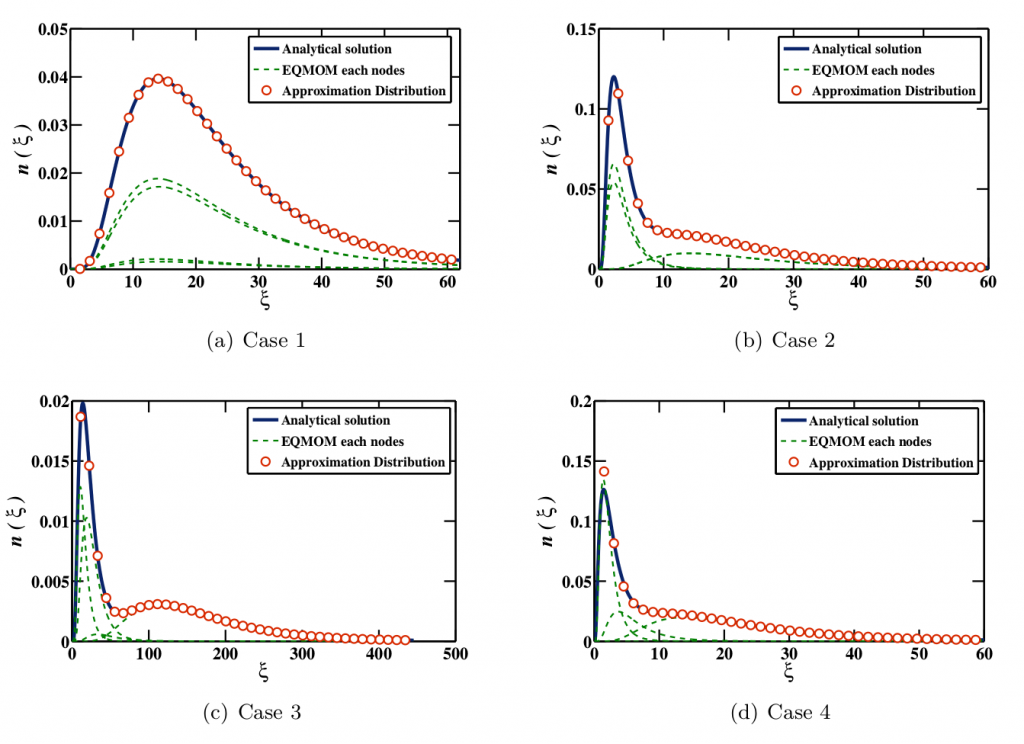
Measurements in the laboratory are often expensive and it might take months to provide these measurements. Thus, computational modeling is a solution for this shortcoming of experimental measurements. There are several approaches that have been presented in the literature that can predict the size of the particles inside the system under study. However, either they are computationally expensive and thus are not attractive to industrial applications, or they have a lack of accuracy. An extended quadrature method of moments (EQMOM) with log-normal kernel density functions is developed in this work and applied to the solution of a population balance equation (PBE) for aggregation and breakup, coalescence, and condensation problems. The cases with one and two kernel density functions are studied analytically, and the existence of an analytical solution is shown. The developed model is accurate and is applicable to the industrial scale measurements.
Journal articles with peer review
- Passalacqua A., Laurent F., Madadi-Kandjani, E., Heylmun J. C. and Fox, R. O. 2018. An open-source quadrature-based population balance solver for OpenFOAM. Chemical Engineering Science 176, 306-318.
- Madadi-Kandjani, E. and Passalacqua A., 2015. An extended quadrature-based moment method with log-normal kernel density functions. Chemical Engineering Science 131, 323-339.
Conference proceedings
Note: The underlined name indicates who presented the work at the conference.
- Madadi-Kandjani, E., Passalacqua, A., 2014. An extended quadrature method of moments with log-normal kernel density functions. AIChE Annual Meeting, At Atlanta, GA.