After a long absence, I am sharing part of my research with you. Earlier this year I tested the functionality of LnEQMOM for problems include the growth of particles with nucleation. This is the work done by me and my advisor Dr. Alberto Passalacqua. Here are some results I want to share with you. For detailed information on how the algorithm of the LnEQMOM works, I recommend you to refer to our paper we published. I hope you enjoy reading it.
Mono-surface growth with Gaussian nucleation
As mentioned at the study, we consider the mono-surface growth of the particles with an initial condition of a log-normal distribution for the particle sizes. The considered log-normal distribution has a mean of μ = 0 and the variance of σ = 1∕2. The distribution that has been considered in the previous study centered at 1. So the initial condition can be written as:
 |
(1) |
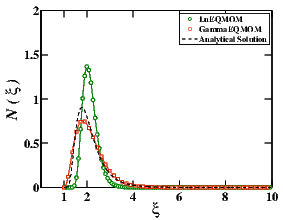
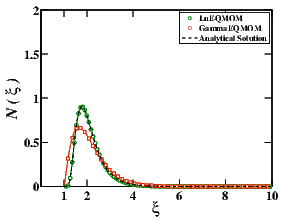
To compare the accuracy of the EQMOM, we first reconstruct the distribution using the moments of the NDF. lognormal EQMOM and γ-EQMOM with different number of the nodes have been considered . As seen on Fig. 1, the results obtained by LnEQMOM predicts the solution pretty good after the N= 2 while γ-EQMOM is accurate by the N= 3. Using the N= 4, γ-EQMOM fails in predicting the accurate results.
Figure 1: Comparison of the reconstructed NDF with LnEQMOM and Gamma EQMOM and the analytical solution, as a function of the number of primary quadrature nodes N.
The moments that have been calculated using these methods has the error of order mentioned at Tab. 1.
| Case | N = 2 | N = 3 | N = 4 | |||
| LnEQMOM | M0 | 5.62 × 10–16 | M0 | 3.36 × 10–16 | M0 | 2.24 × 10–16 |
| M1 | 6.82 × 10–16 | M1 | 1.01 × 10–16 | M1 | 1.70 × 10–16 | |
| M2 | 1.28 × 10–15 | M2 | 8.53 × 10–16 | M2 | 1.01 × 10–16 | |
| M3 | 1.99 × 10–15 | M3 | 9.99 × 10–16 | M3 | 1.11 × 10–16 | |
| M4 | 1.01 × 10–16 | M4 | 1.93 × 10–15 | M4 | 1.93 × 10–16 | |
| M5 | 2.68 × 10–15 | M5 | 2.82 × 10–16 | |||
| M6 | 5.36 × 10–16 | M6 | 5.36 × 10–16 | |||
| M7 | 1.22 × 10–15 | |||||
| M8 | 8.56 × 10–16 | |||||
| gammaEQMOM | M0 | 1.12 × 10–16 | M0 | 4.49 × 10–16 | M0 | 2.24 × 10–16 |
| M1 | 1.71 × 10–16 | M1 | 3.41 × 10–16 | M1 | 1.01 × 10–16 | |
| M2 | 2.13 × 10–16 | M2 | 1.01 × 10–16 | M2 | 2.13 × 10–16 | |
| M3 | 4.44 × 10–16 | M3 | 5.55 × 10–16 | M3 | 3.33 × 10–16 | |
| M4 | 5.79 × 10–16 | M4 | 3.86 × 10–16 | M4 | 7.72 × 10–16 | |
| M5 | 1.01 × 10–16 | M5 | 8.47 × 10–16 | |||
| M6 | 7.15 × 10–16 | M6 | 7.15 × 10–16 | |||
| M7 | 1.02 × 10–15 | |||||
| M8 | 2.57 × 10–15 | |||||
Table 1: Relative error affecting the moments of the reconstructed distribution as a function of the number of primary nodes N.